|
Measurements of magnetic moments are valuable tools in nuclear
structure studies since, due to the big differences between the
g factors of protons and neutrons, they are sensitive to single
nucleon contributions to wave functions and their interplay with
collective degrees of freedom. Interesting measurements can be
performed in nuclei near closed shells, nuclei where the
interplay between collective and single nucleon degrees of
freedom is strong, high spin states of nuclei where the
back-bending phenomenon occurs, and nuclei close to the drip
lines where new phenomena are apparent, as the disappearing of
magic numbers and the appearing of new ones. Most of the above
states are short lived and their measurement should be
accomplished through special techniques.
In general nuclear magnetic moments can be
measured through their interactions with magnetic fields. In
order to achieve the appropriate precision, hyperfine fields
obtained through interactions between nuclei and their own
atomic electrons, or the electrons in the solids, which they
transverse must rather be used instead of the laboratory fields.
In particular, the magnetic hyperfine
interaction, between a moving ion and the ferromagnetic
environment in which it moves (transient magnetic fields), has
been the subject of many studies in the borders of atomic and
nuclear physics, while its application to magnetic moment
measurements has produced numerous valuable results. The main
features of a typical experimental set up are shown in the
figure.
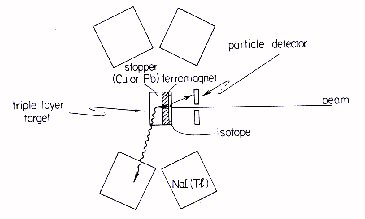
In most experiments, the state of interest
is created preferentially by Coulomb excitation (of the beam or
the target nuclei) or heavy ion fusion reactions. The excited
ions recoil through a thin ferromagnetic material and stop in a
thick backing where they are not subject to any further
hyperfine interactions. Four gamma detectors are located at an
angle theta, where the slope in the angular distribution of the
decay gamma radiation is maximum. The ferromagnet is polarized
either up or down by a small magnetic field and the gamma
counting rate is recorded as a function of field direction. An
effect, ε, is determined and finally the
rotation of the magnetic moment which is manifested through the
rotation of the distribution.
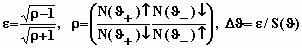
Where ε is the effect, S(θ) the slope of
the distribution and Δθ the rotation of the
distribution and thus the rotation of the magnetic moment. The rotation is
connected with the applied transient field, and the g-factor of the state
through the following relation:
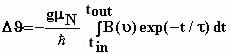
The transient field is given through parametrizations as a function of the ion velocity and the magnetization of the
ferromagnetic material. Details of the technique and the field
origin as well as
its parametrization can be found in the article by
Benczer-Koller, Hass and Sak
in Ann. Rev. Nucl. Part. Sci. 30 (1980) 53.
One of the members of the NPL was specialized to such
measurements and a series of articles can be found in A. Pakou's CV. |
![]()

